Latin Square and Sudoku Solver Using SAT Solver (JavaScript logic-solver)

JavaScript Sudoku Math Combinatorics Latin_Square Puzzle SAT Solver

---

Posted on Nov 24

---

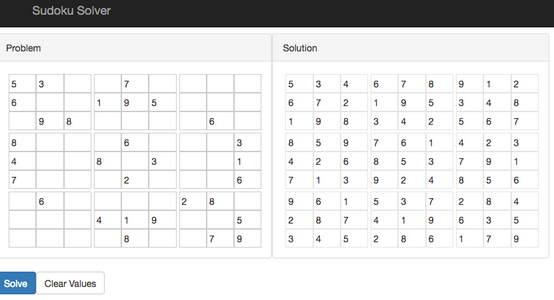
Latin squares and Sudoku programatically generated are show below. These are screenshots of web apps created using JavaScript and a SAT solver library.

Example: Latin Squares 1 of size 5

Example: Sudoku 2

These problems can be expressed as Boolean satisfiability problems (SAT) ³ and solved using a SAT solver.

I chose the logic-solver⁴ JavaScript library to solve Latin squares and Sudoku. The central part of the program is listed below. More details will follow later in this page.

// solver: an instance of Logic.Solver where Logic is the logic-solver module.
// vars: a multi-dimensional (n x n x n) array of variable names.
// range: a utility function to make an array of integers from 1 to n.
function latinSquare(solver, vars) {
  const n = vars.length;
  range(n).forEach((i) => {
    range(n).forEach((j) => {
      solver.require(Logic.exactlyOne(range(n).map((k) => (vars[k][i][j]))));
      solver.require(Logic.exactlyOne(range(n).map((k) => (vars[i][k][j]))));
      solver.require(Logic.exactlyOne(range(n).map((k) => (vars[i][j][k]))));
    });
  });
}

function sudoku(solver, vars) {
  const n = vars.length;
  const m = Math.floor(Math.sqrt(n));
  latinSquare(solver, vars);
  range(m).forEach((i) => {
    range(m).forEach((j) => {
      range(n).forEach((k) => {
        solver.require(Logic.exactlyOne(
          range(n).map((l) => (
            vars[m*i + Math.floor(l/m)][m*j + (l%m)][k]
          ))));
      });
    });
  });
}

Sample Apps

• sat-latin-square
• sat-sudoku-solver

How to Run the Apps

To run the apps, Node.js is required. Each demo app runs as a server and can be launched as below:

# Correct the following placeholders REPO and THE_DIR_OF_CLONED_REPO.
git clone $REPO
cd $THE_DIR_OF_CLONED_REPO
yarn install
yarn run start

The app can be accessed via a web browser. The default port is 3000.

The Latin squares demo (sat-latin-square) has a form to enter a problem size (from 2 to 6). It starts generating (reduced) Latin squares of given size upon submission of the form. To avoid heavy computational load, not all the solutions are shown.

The Sudoku demo (sat-sudoku-solver) has two grids. A partial assignment can be specified on the left grid. The solver starts upon pressing the Solve button and shows a solution, if any, on the right grid.

Usage of logic-solver in the Apps

I use a variable Logic to refer to the module logic-solver.

const Logic = require('logic-solver');

Before constructing logical constraints, some utility functions are defined. The range function generates an array containing integers ranging from zero to n-1.

function range(n) {
  return Array(n).fill().map((x, i) => (i));
}

The genVars function generates variable names each of which is indexed by a triple (r, c, s) where r, c and s each indicates a row index, a column index and a symbol respectively. An index has the dimension of size x size x size. A pair (r, c) specifies a cell in a Latin square. Only one variable for each cell can have a true value. A set of (r, c, s) triples for all the true variables is the orthogonal array representation of a Latin square.

function genVars(prefix, size) {
  return range(size).map((i) => (
    range(size).map((j) => (
      range(size).map((k) => (
        [prefix, i.toString(), j.toString(), k.toString()].join('_')
      ))
    ))
  ));
}

A Latin square is an n x n array filled with n different symbols. The function latinSquare constructs a logical formula expressing the conjunction of the following logical conditions

• Each symbol must occur exactly once in each column.
• Each symbol must occur exactly once in each row.
• Each cell of a square must have exactly one symbol.

The exactlyOne function returns an expression requiring that only one of the variables given must be true and thus can be used to express each one of the above conditions. The require method is called to instruct the solver that the given condition must be met to satisfy the whole logical formula.

// vars = genVars('v', n)
function latinSquare(solver, vars) {
  const n = vars.length;
  range(n).forEach((i) => {
    range(n).forEach((j) => {
      solver.require(Logic.exactlyOne(range(n).map((k) => (vars[k][i][j]))));
      solver.require(Logic.exactlyOne(range(n).map((k) => (vars[i][k][j]))));
      solver.require(Logic.exactlyOne(range(n).map((k) => (vars[i][j][k]))));
    });
  });
}

Finally, Sudoku is defined as a Latin square with an additional alldifferent constraint on each subgrid that has the dimension m x m where m x m = n.

function sudoku(solver, vars) {
  const n = vars.length;
  const m = Math.floor(Math.sqrt(n));
  latinSquare(solver, vars);
  range(m).forEach((i) => {
    range(m).forEach((j) => {
      range(n).forEach((k) => {
        solver.require(Logic.exactlyOne(
          range(n).map((l) => (
            vars[m*i + Math.floor(l/m)][m*j + (l%m)][k]
          ))));
      });
    });
  });
}

Running the (Sudoku) solver and obtaining a possible solution is as trivial as the following snippet:

    const n = 9;
    const solver = new Logic.Solver();
    sudoku(solver, genVars('v', n));
    const solution = solver.solve();

If no solutions are found, solution is null. Using this fact allows us to get all the possible solutions by iterating the solve() method until it returns null.

An assignment that satisfies the constraints can be obtained by using the solution.getMap() method that returns a dictionary object that maps a variable name to its Boolean value assignment.

---

I am really impressed at how useful a SAT solver can be. Latin squares (and Sudoku) seemed to me really complex at first but can be expressed very concisely with logic-solver. I am wondering whether I want to further study this interesting technology instead of just purposelessly producing toy programs like above.

References

---

2015 My gh-pages